模拟电路设计系列讲座六：二阶系统之瞬态响应

2019-01-28 09:55

一：瞬态响应基本介绍

如下图所示的LCR二阶振荡系统，我们假设电阻足够小，系统处于欠阻尼状态，由系列讲座五我们知道此系统有两个复平面极点。

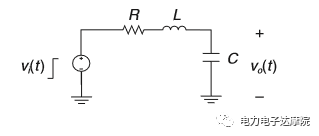
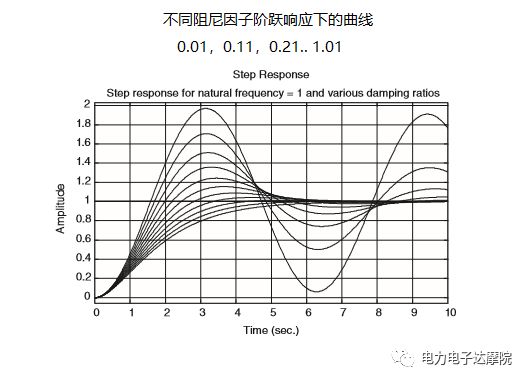
单位阶跃响应如下：

单位阶跃响应的峰值表达式如下：

比如，对于阻尼因子为0.2的系统，振荡的峰值约为1.6倍。

二：增加额外高频极点对于二阶系统的影响

如果二阶系统增加一个或者多个极点，对系统有何影响？这取决于增加的极点离谐振频率ωn的远近。之前我们讲过，高频极点相当于幅值为1，负的相移-近似随频率的增加而减少（对应于时延）。

下图实线表示自然振荡频率ωn=1 radian/second, 阻尼因子ζ=0.5的阶跃响应曲线。虚线表示增加了额外高频极点-10 radian/second的阶跃响应曲线。可以看出这两个曲线基本重合，只是上升时间阶段，增加了额外极点的系统延时了0.1s，原因就是增加的高频极点带来的延时。

如果增加的额外极点位于-2 radian/second，增加了此极点的系统延时就比较明显了，原因是增加的额外极点的频率没有那么高。虚线就是增加了额外极点的阶跃响应曲线。

由以上讨论可知，对于一个三阶振荡系统，如果最高频率是谐振频率的10倍以上，我们就可以忽略最高频率，系统可以等效成二阶振荡系统。

声明： 本文由入驻维科号的作者撰写，观点仅代表作者本人，不代表OFweek立场。如有侵权或其他问题，请联系举报。

共0条评论，0人参与

登录登录即可访问所有OFweek服务

请输入评论内容...

请输入评论/评论长度6~500个字

暂无评论

图片新闻

行业报告